「ポートフォリオの作り方:最大損失の目安を算出する方法」の中で、ポートフォリオにおけるリターンとリスクについて書きました。
また、リターンとリスクを正規分布という統計上の考え方に当てはめることで、最大損失の目安を算出する方法について解説しました。
今回はリターンとリスクが長期的にどのように推移していくのかを考えてみます。また、正規分布を活用してポートフォリオが元本割れする確率を算出する方法について解説し、元本割れする確率が長期的にどのように推移するのかについて、検証していきます。
リターンとリスクの定義。
「ポートフォリオの作り方:最大損失の目安を算出する方法」の中で書きましたリターンとリスクの定義について、簡単にまとめておきます。
・リターン:将来の期待収益率。年率に換算した利回りで表す。
・リスク:価格のブレ幅の大きさ。年間増減率の度合いを標準偏差で表す。
リターンとリスクは、いずれも1年当たりの平均値を数値化したものです。
では、この二つは年を追うごとにどのように推移していくのでしょうか。
以下、リターン5%、リスク20%の資産を例に、検証していきます。
2年後、10年後、20年後のリターンの計算
2年度、10年後、20年後のリターンの計算は、年率複利計算を積み上げたものとなります。
1年後の平均リターンが5%の資産を複利で運用すると、100投資した資産は1年後には「100×1.05=105」、2年後には「105×1.05=110.25」となります。
2年で10.25の増加ですので、2年後のリターンは10.25%となります。
10年後には1.05倍を10回繰り返すことになりますので、100投資した資産は「100×1.05の10乗=162.89」となります。
10年で62.89の増加ですので、10年後のリターンは62.89%となります。
20年後には1.05倍を20回繰り返すことになりますので、100投資した資産は「100×1.05の20乗=265.33」となります。
20年で165.33の増加ですので、20年後のリターンは165.33%となります。
2年後、10年後、20年後のリスクの計算
2年後、10年後、20年後のリスクの計算については、野村證券の証券用語解説集における「標準偏差・分散」の解説を参考にします。
その解説には、日次、週次、月次の標準偏差を年換算するための計算方法が記載されており、日数、週数、月数の平方根を掛けた値が年率換算値になる、と書いてあります。これを応用すると、年次の標準偏差を2年後、10年後、20年後に換算するためには、それぞれ2の平方根、10の平方根、20の平方根を掛けた値にすればよい、ということになります。
2の平方根は1.41、10の平方根は3.16、20の平方根は4.47です。
1年のリスクが20%の資産は、上のそれぞれの平方根の値を20%に掛けた結果、2年後のリスクは28.2%、10年後のリスクは63.2%、20年後のリスクは89.4%という計算結果となります。
正規分布のグラフは保有期間に対し、どのように変化していくか。
まず、1年後のリターンが5%、リスクが20%の正規分布のグラフは下の通りです。

この資産は上で計算した通り、2年後にはリターンが10.25%、リスクが28.2%の資産となります。これを正規分布のグラフにして1年後と重ねると、下のグラフのようになります。

1年後→2年後で、リターンが増加した分、グラフの山の頂上が横軸の右側に動いたことが分かります。
また、リスクが増加した分、グラフの山の頂上が低くなり、すそ野が広がったことが分かります。
この資産は10年後はリターン62.89%、リスク63.2%。20年後はリターン165.33%、リスク89.4%と推移していきますので、10年後と20年後の正規分布をさらに重ね合わせると、下のグラフのようになります。
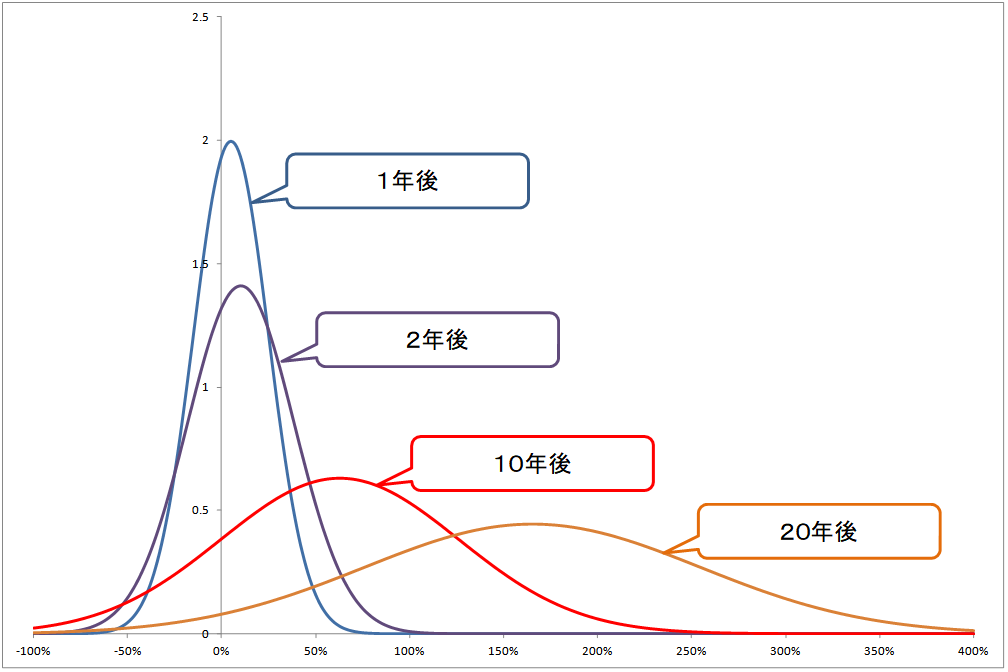
10年後、20年後と、保有期間が長くなるにしたがって、平均リターンが高くなることで、グラフの山の頂上は横軸の右側に動いていきます。
また、保有期間が長くなるにしたがって、リスクが増大することで、グラフの山の形はなだらかに広がっていき、分布が平均値から散らばっていくことが分かります。
元本割れ確率の試算方法。
それぞれのグラフで、横軸が0%未満となる部分が元本割れとなる分布の範囲です。下のグラフで薄いグレーの部分に重なる範囲となります。
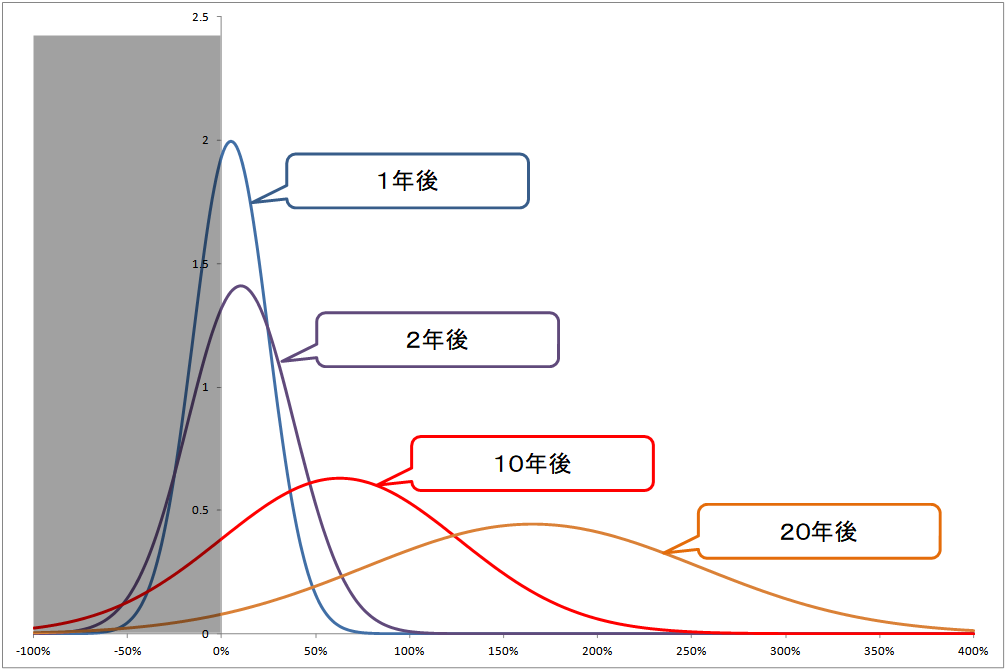
この部分の出現確率は、1年後>2年後>10年後>20年後と、保有期間が長くなるに連れて次第に小さくなっていくことが視覚的に一目でお分かりいただけると思います。
この確率の計算は、マイナスからちょうど0%になるまでの分布を累積し、それが全体の分布のうちの何%に当たるかを算出すればよい、ということになります。
Excelの計算式を使うと、NORMDIST(0,平均値,標準偏差,TRUE)で求められます。
平均値にはリターンの値を、標準偏差にはリスクの値をそれぞれ入力します。(5%→0.05など、%単位の値は百分の一で入力)
これによる元本割れ確率の計算結果は、
1年後:NORMDIST(0,0.05,0.2,TRUE)=40.13%
2年後:NORMDIST(0,0.1025,0.282,TRUE)=35.85%
10年後:NORMDIST(0,0.6289,0.632,TRUE)=16.00%
20年後:NORMDIST(0,1.6533,0.894,TRUE)=3.23%
となります。(四捨五入の関係で多少の誤差があります)
数式の最初の値に0を入力したのは、0%になるまでの分布の確率を計算するためです。ですので、例えば「20年後に10%の資産増加率を獲得できない確率」を計算したい場合は、ここに「0.1」を入力すれば、答えが得られます。
グラフでも視覚的に何となくお分かりいただけたと思いますが、改めて計算結果を見ると、この資産は20年保有すれば元本割れの心配はほとんどなさそうだ、と判断しても良さそうな確率となります。
この資産ポートフォリオの前提はリターン5%、リスク20%でしたが、これは平均的な先進国株式インデックスのリターンとリスクに近い数値を例にしています。
この試算結果だけ見ると、20年保有できるのであれば、先進国株式インデックス100%のポートフォリオを組めば、他の資産クラスへの分散投資をせずとも十分な運用成果が出そうな気になってきます。
ただし、リスク値が大きい資産は最大損失の目安が大きくなってしまう、ということも考慮する必要はあります。
まとめ
リターンも想定値、リスクも想定値、その分布が正規分布に従うというのも仮説、という何とも頼りない前提ではあります。
しかしながら、統計的な検証としては一定の目安にはなります。少なくとも、長く保有すればするほど、元本割れ確率が小さくなっていくという結果については、安心感があるのではないでしょうか。
自分のポートフォリオから元本割れ確率の目安を算出できる、ということを知るだけでも、長期保有についての気持ちが前向きなものになると思います。
そして、日々の値動きに一喜一憂せず、暴落しても慌てずに耐え、気長に上昇を待つことができるような、長期目線の資産運用に向けての好材料になると考えます。
何よりも、Excelがあれば数式一つで簡単に結果が出ますので、手間もコストもほとんどかけずに算出できます。是非活用していただきたいと思います。Mr.老眼も日々学び、実践していきます。


