「資産運用の基本その2:分散投資のメリット」の中で、分散投資の有用性について書きました。
その記事にも書いた通り、分散投資とは「失っても良いと思える金額はいくらか?」を出発点にするのが本来のあり方だと考えます。株式投資のリスクを具体的な金額で把握する必要があるということです。
ここでは資産運用におけるポートフォリオの考え方と、ポートフォリオにおける最大損失額の算出、自分に見合うポートフォリオの作り方について書いていきます。
ポートフォリオとは?
資産運用において、リターン(期待収益率)やリスク(価格のばらつき度)の異なる複数の資産クラスを組み合わせて保有する際の、その資産の組み合わせの配分をポートフォリオと言います。
例えば株式を5割、債券を3割、残りの2割を普通預金、といった配分がポートフォリオです。
ポートフォリオを管理する意義とは、自分の求めるリターンと、自分が受け入れられるリスクとのバランスを把握し、コントロールすることです。
そのためには、ポートフォリオを検証する際に欠かせない、リターンとリスクの定義をしっかり把握しておく必要があります。
リターンとは何か。
リターンとは、その資産の将来の期待収益率のことです。一般に年率に換算した利回りで表されます。
例えば日経平均株価の期待収益率が5%だと仮定したときに、日経平均株価に100投資したとすると、1年後には105になると期待できる、ということです。
このリターンは複利と考えられますので、複数年ですと「1.05×年数分」で資産が増えていくと期待できることになります。
例えば日経平均株価に100投資したとすると、2年後には100×1.05×1.05=110.25になると期待できる、ということです。
利息にも利回りが乗るという複利の考え方は、資産運用にとって重要な考え方なのでしっかり確認しておきましょう。
また株式投資では価格の上昇による収益に加え、配当金による収入を期待できます。株式における期待収益率は、価格上昇分と配当金収入分を合計した総合利回りを指します。
分配金収入がある債券や不動産も同様に考えます。
分配金収入が発生しないコモディティは価格上昇分のみを期待収益率と考えます。
リターンの考え方自体はこのように難しいものではありませんが、資産運用にあたり実際に資産のリターンをいくらに設定するのか、という問題は簡単ではありません。過去の傾向から類推するという方法の信頼度が、決して高くないからです。
下の表はMr.老眼が自分のポートフォリオに関連する資産のリターンを、過去実績を参考に算出したものですが、どうやら将来予測に当てはめるには頼りないくらいバラバラな結果です。過去の期間の取り方ひとつで全然違う結果になっています。
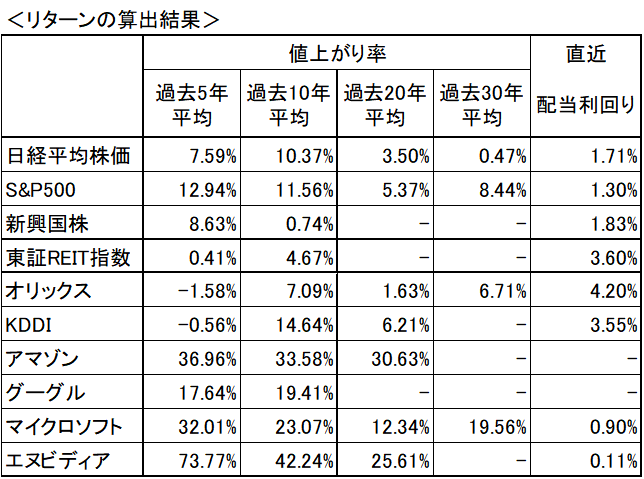
個別の投資案件では、将来の収益見積もりからリターンを求める手法があり、信頼度は比較的高いものになります。
しかしながら、資産運用においては将来の収益見積もりを作成できるような情報を個人投資家が入手するのはほとんど不可能ですので、この方法は取れません。
年金積立金管理運用独立行政法人(GPIF)やJPモルガンなど資産クラスのリターン前提を公開している機関もあります。過去の推移と見比べつつ、ポートフォリオ管理に活用できる重要な情報の一つと考えます。
リスクとは何か。
リスクとは、資産の価格のばらつき度のことです。価格変動のブレ幅の大きさ、といった意味です。とは言っても、ばらつき度を数値化するという考え方が一般的ではないかもしれません。
高校の数学で習う分散と標準偏差を使うのですが、Mr.老眼は習ったことさえ覚えていませんでした。
ただ、馴染みがないだけで、具体例で理解すれば全然難しくありませんので、分散と標準偏差について、例をあげて説明していきます。
平均身長170cmの3人グループの分散と標準偏差の計算例
169cm、170cm、171cmの3人の場合:
それぞれの平均との差は-1cm、±0cm、+1cmです。
分散の計算は平均差の2乗の総和を平均したものです。計算方法は「(-1²+0²+1²)÷3≒0.67」となります。
標準偏差は分散の平方根を計算した数値です。上の例ですと「√0.67≒0.82」となります。
160cm、170cm、180cmの3人の場合:
それぞれの平均との差は-10cm、±0cm、+10cmです。分散の計算方法は「(-10²+0²+10²)÷3≒66.67」となります。
標準偏差は「√66.67≒8.16」となります。
このように、同じ平均身長の3人グループでも、平均との差が大きいグループの方が標準偏差が大きくなります。ばらつき度が大きければ標準偏差が大きいということです。
この標準偏差の値を投資資産の価格変動にそのまま当てはめたのがリスクの数値化です。
投資資産のリスク(価格のばらつき度)の数値化
例えば、100投資した資産が1年後に120、2年後に110、3年後に115になっていたとします。
それぞれの前年比の増減率は+20.00%、-8.33%、+4.55%です。平均は+5.40%となります。
平均との差は1年目が+14.60%、2年目が-13.74%、3年目が-0.86%です。
計算式は上記の例と同様のため省略しますが、この例における分散は0.0134、標準偏差は0.1158となります。この標準偏差を変動率の%単位で表すと11.58%ですが、これがこの資産の1年当たりのリスク値となります。
リスク値の活用方法と具体的な設定
リスクを数値化するために標準偏差の考え方を使っているということを説明してきました。ここで二つの疑問が想像できます。
質問1:この数値化にどのような活用方法があるのか?
質問2:自分のポートフォリオにどのように適用できるのか?
質問1についてですが、リスクが標準偏差で表されていることによって得られるメリットの一つは、正規分布という統計モデルに当てはめることで、自分のポートフォリオの最大損失額の目安を知ることができる、というものです。この記事の後半でこの計算方法を説明していきます。
質問2についてですが、リスクの数値には過去の傾向にある程度の信頼性があります。
下の表はMr.老眼が自分のポートフォリオに関連する資産のリスク値を過去実績を参考に算出したものです。データを取る年数によってリスク値は変わってきますが、リターンに比べて傾向値に納得感があります。
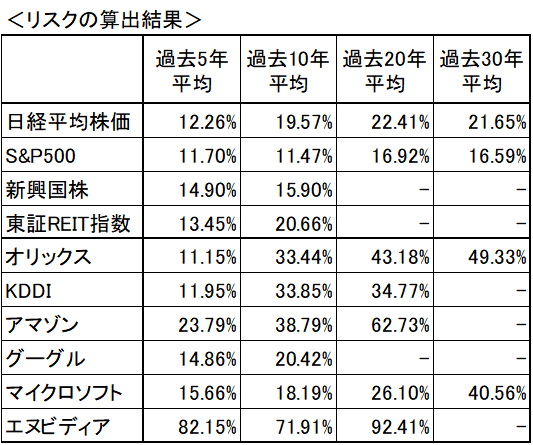
ただし個別株だと極端な値が出てしまうのが分かります。個別株は資産運用に向いていないというのがMr.老眼の見解ですが、その理由の一つが、こういった試算根拠の値がつかみにくい、というところにあります。
なお、自分の保有銘柄について、リスク値を設定するにはいくつかの方法があります。
Mr.老眼のように自分で各銘柄の値動きをネットで集め、エクセルで計算するのも一つの方法です。
アメリカのETFについては、米国ヤフーファイナンスの各ETFの詳細ページに過去3年・5年・10年のリスク値が掲載されています(Standard Deviationという欄)。
大まかな目途で良ければ、株式インデックスは20%、個別銘柄は35%、債券は10%、REITインデックスは20%、といった水準で簡易計算してみるというのも割り切りとしては有りだと思います。あくまでも目安を知るためのツールですので。
ポートフォリオにおけるリターンとリスクの算出方法
ポートフォリオにおけるリターンとリスクの算出方法について説明します。
といっても、リターンとリスクの考え方を理解してしまえば、後は簡単です。
要は資産ごとのリターンとリスクを設定し、所有資産全体との割合で加重平均するだけです。例えば以下のように各資産のリターンとリスクを設定したとします。
株式:リターン5%、リスク20%
債券:リターン1%、リスク10%
株式60%、債券40%のポートフォリオを組んだ場合:
ポートフォリオ全体のリターンは「(5%×60%)+(1%×40%)=3.4%」
ポートフォリオ全体のリスクは「(20%×60%)+(10%×40%)=16%」
となり、リターン3.4%、リスク16%の資産に投資しているのと同じ効果があるということになります。
これを株式50%、債券50%のポートフォリオに変更すると、リターン3.0%、リスク15%に変わります。
このように、ポートフォリオ全体のリターンとリスクが、資産の保有割合によって変化していくことを理解しておきましょう。
最大損失の目安を算出する方法
ここまででポートフォリオ全体のリターンとリスクを算出しました。
リスクは標準偏差を表していることは上述の通りですが、標準偏差は正規分布という統計上の考え方を使って活用できます。
正規分布とは、平均値が最頻値かつ中央値であるような集団で、かつ平均より上にも下にも同じような分布がある集団の分布をモデル化したものです。
言葉で説明してもイメージが湧かないと思います。下のグラフが正規分布のグラフです。
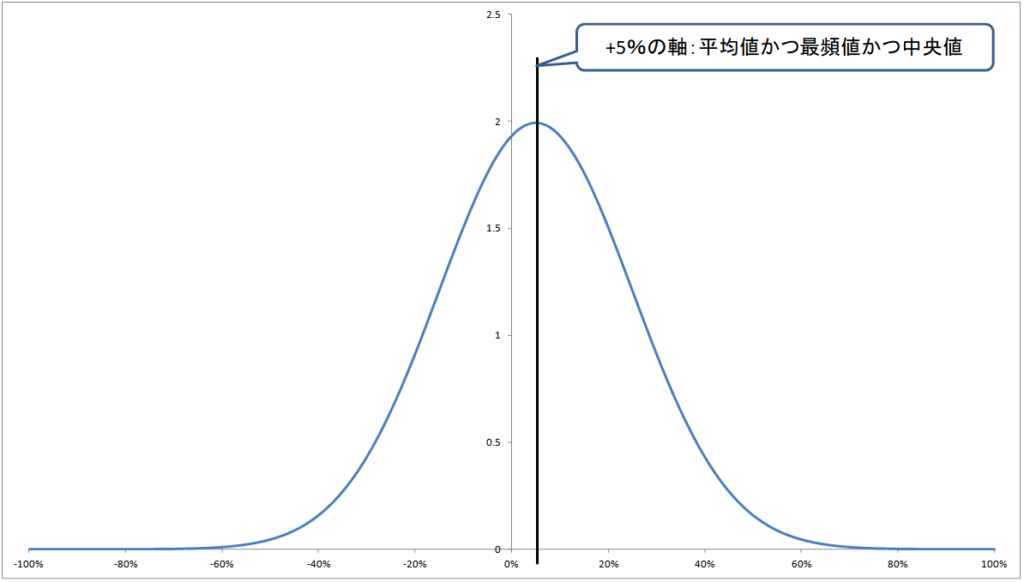
横軸5%が平均となる分布図のグラフです。平均値が最も高く(=最も分布が多い最頻値である)、平均値の左右に均等にすそ野が広がっている(=平均値が中央値でもある)ことがグラフを見ると分かると思います。
この分布は確率論から得られる分布の一つですが、この正規分布という分布は自然現象や社会現象に当てはまることが多い分布とされています。
もし投資資産の値動きがこの正規分布に当てはまるとしたら、平均から大きく外れる確率は低いはずだ、ということになります。非常に頼りない仮定ではあるのですが、何らかの目安にはなるだろう、ということで、正規分布を活用してポートフォリオを分析するという手法を紹介します。
リターン5%の資産があると仮定します。このリターン5%というのは平均すると毎年5%の利回りが期待できる、という意味です。
この資産のリターンが正規分布のような分布に従うと仮定すると、毎年のリターンは5%という平均値から大きく外れる確率は次第に低くなっていくはずだ、ということになります。平均値±10%動くことはある程度可能性はあっても、平均値±50%も値が動く可能性は小さいだろう、ということです。
ここで、価格のばらつき度であるリスク値に標準偏差を使っていることが威力を発揮します。というのも、正規分布と標準偏差の値には、下のグラフのような関係があるとされているからです。
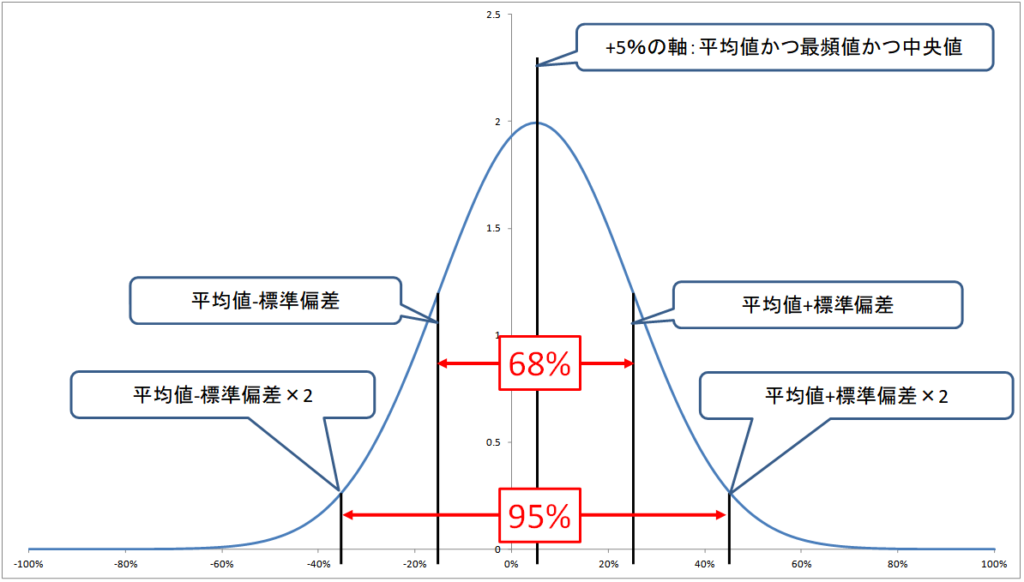
正規分布では、「平均値±標準偏差」の中に分布が含まれる可能性が約68%、「平均値±標準偏差の2倍」の中に分布が含まれる可能性が約95%である、という統計上の性質があります。
ということは、「平均値±標準偏差の2倍」に収まらない数字が出現する可能性は約5%しかありません。その5%には上に外れる場合と下に外れる場合の両方を含みますので、下に外れる確率はその半分、つまり約2.5%しかない、というわけです。
この統計上の性質を、リターン5%、リスク20%のポートフォリオに当てはめてみましょう。
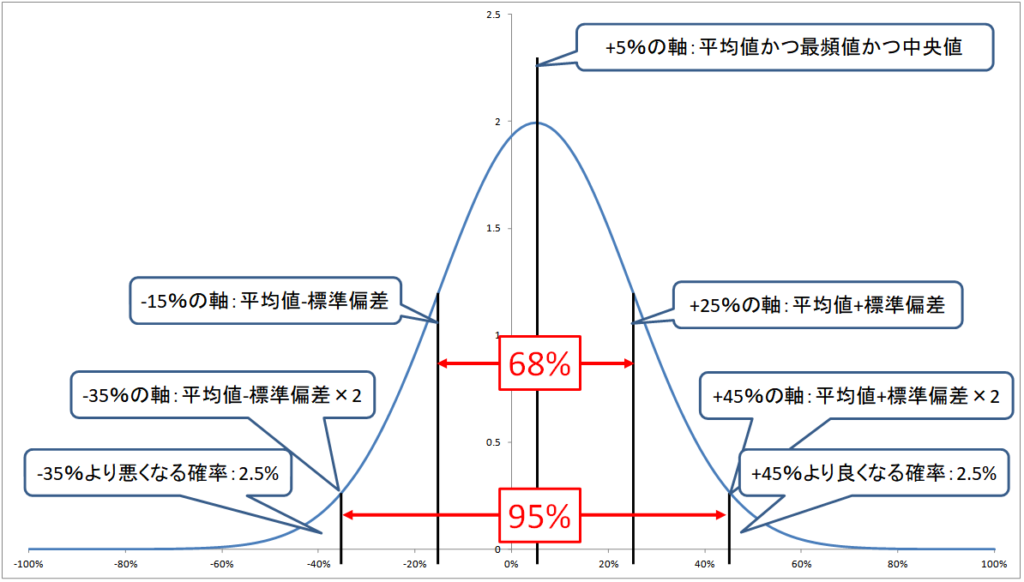
「平均値±標準偏差の2倍」というのは、「5%±20%×2」ですので、上は+45%、下は-35%です。ということは、このポートフォリオで1年後にマイナスの運用成績で35%以上目減りする確率は約2.5%しかない、ということになります。
2.5%は1/40ですので、40年に一度の確率しかない、ということです。
最大損失の目安としては、「平均リターン-リスクの2倍」の下落率を覚悟しておけばよさそうだ、というように活用できるのです。
正規分布をポートフォリオに当てはめるこの方法は、Mr.老眼が自力で編み出したわけでもなんでもなく、実はファイナンシャルプランナー2級の教科書に載っているものです。
にもかかわらず、資産運用の説明でこの考え方に触れているものはあまり見たことがありませんので、ポートフォリオの作り方の一環としてご紹介しました。
楽天証券の山崎元さんが、「ホンネの投資教室」という連載の中で、この考え方について度々言及されています。Mr.老眼は楽天証券に口座を持っていませんので、大変申し訳なく思いながら、この連載をしばしば参考にしています。
まとめ:自分に合ったポートフォリオとは
運用効率だけを考えれば、あるべきポートフォリオというのは似通ったものになります。
しかしながら、自分に合ったポートフォリオというのは人それぞれ違います。何故なら、「失っても良いと思える金額」が人によって違うからです。
それは運用資産の規模による違いに加え、その人の性格による違いが大きいと思います。
また投資経験による値動きへの慣れにも個人差があります。
値動きの大きさに慣れ、大きな目減りも長期的には回復していくという経験を既にしている人は、最大損失が大きいポートフォリオを組むことができます。
一方、投資を始めたばかりで大きな目減りは精神的に耐えられないという方は、最大損失が大きいポートフォリオを組まない方が良いと思います。
いずれにしても、下がっても我慢して保有すべきと言うからには、最悪どの程度まで下がるのかという我慢の目安は必要です。今回はその目安の算出方法についてご紹介しましたので、是非活用していただきたいと思います。Mr.老眼も日々学び、実践していきます。


